One day, you find yourself in a dungeon. Looking around, you see the lock to get out. Underneath the lock, there is a puzzle:
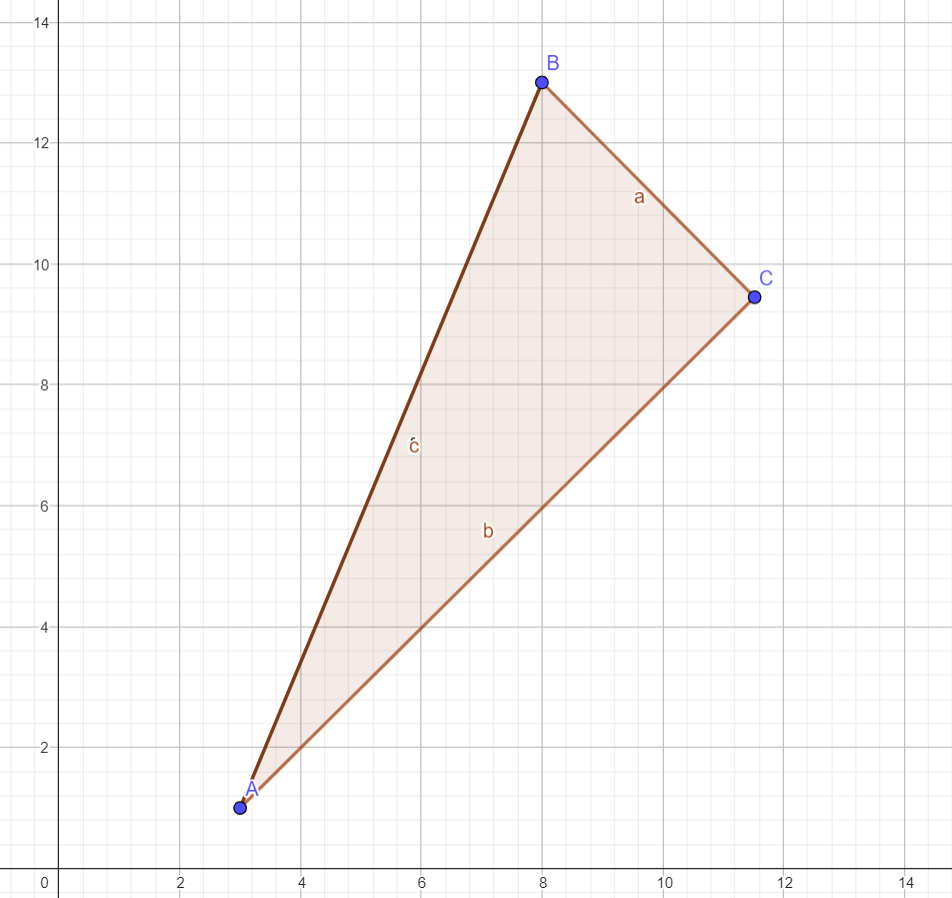
Intrigued by the puzzle, you wonder if there was a way to perform a rotation and dilation on such that you create , one of the legs of the triangle. Then, it hits you: use the complex plane! The coordinates on the coordinate plane correspond to the point on the complex plane. Namely, the x-value corresponds to the real component and the y-value corresponds to the imaginary component. The point is written in rectangular form, and has nice properties when dealing with rotations and dilations. For examples, rotations can be dealt with using Euler’s Formula.
Rotations on the Complex Plane
Euler’s Formula states that
Unfortunately, a proof of this formula will be beyond the scope of this article.
Let’s say that you have the point . In rectangular form, the point is expressed as . On the complex plane, this is the same point as the angle on the unit circle in the complex plane. To get from angle to angle , we need perform a transformation on such that the argument (the angle) becomes . By complex number multiplication, we multiply to to get . Thus, to rotate point counterclockwise about the origin by , we multiply it by , or .
Dilations on the Complex Plane
Now, let’s explore dilations. Let’s start again with a point on the complex plane, namely, . Since the magnitude of is , the magnitude of is . We want to dilate the point such that the magnitude is now . Thus, we multiply by to get
Thus, to dilate a point such that the magnitude becomes , we multiply it by .
Solving the Puzzle
With the power of the complex plane, we are able to rotate and then dilate to create . To rotate , we first transform such that lies on the origin. Otherwise, we are rotating around the origin, instead of with respect to . Thus, we subtract from all points to get that A’ = (0, 0) and B’ = (5, 12). Then, we translate this onto the complex plane to get that A’ = 0 and B’ = 5+12i.
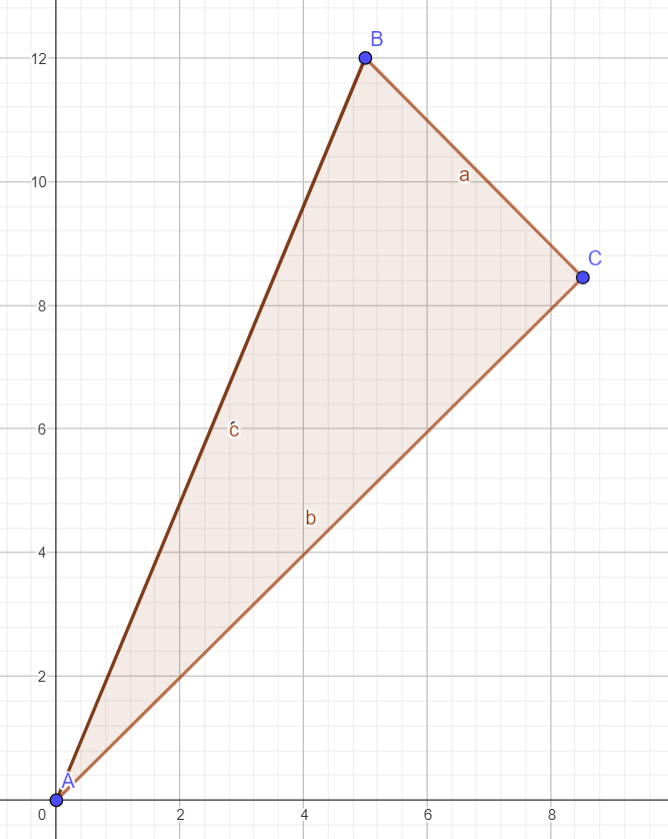
To rotate to , we need to rotate by angle clockwise around the origin. Let be . Since , and . However, since we are rotating by an angle clockwise, we are multiplying by . On the unit circle, a negated angle has the same cosine but opposite sine. Thus, . Then, we are multiplying by . Simplifying, we get
Next, we dilate B’ such that magnitude matches that of what C’ should be. Since |B’| = 13 and |C’| = 12, we multiply by to get that the coordinates of C’ are
Lastly, we translate C’ back to the original spot by adding , or to every coordinate to get that the coordinates of in rectangular form are
Thus, the coordinates of on the coordinate plane is . Suddenly, a floating iPad comes into existence in front of you, just in time for you to type in the coordinates and open the door. We have conquered a puzzle using the power of the complex plane!